问题描述:
如图所示,水平面上的O点处并放着AB两个物体,在A的左侧距A距离为x0处有一竖直挡板,AB之间有少量的炸药.爆炸后B以v2=2m/s的速度向右做匀减速运动;A以v1=4m/s的速率向左匀减速运动,运动到挡板后与挡板发生时间极短的碰撞,碰撞后以碰撞前的速率返回.已知AB在运动过程中加速度大小均为a=2m/s2,方向与物体的运动方向始终相反,AB两物体均视为质点.计算: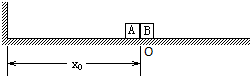
(1)爆炸后向B物体向右运动的最大位移
(2)x0满足什么条件,A物体刚好能回O点
(3)若x0满足什么条件时,A物体能追上B物体.
(1)B物体向右减速至静止时位移最大,由 0-v22=-2ax2 得:x2=
| ||
| 2a |
| 22 |
| 2×2 |
(2)A物体向左运动到挡板时的速度大小为v,则向左减速时有:v2-v12=-2ax0
与碰撞后向右减速恰好到达O点,有:0-v2=-2ax0
联立代人数据解得:x0=2m
(3)当A物体与挡板碰撞后向右减速到达O点的速度为不小于2m/s,A物体能追上B物体.有:v22-v12=-2ax0
代入数据解得:x0=1.5m
答:(1)爆炸后向B物体向右运动的最大位移是1m.
(2)x0满足x0=2m 时,A物体刚好能回O点.
(3)若x0满足x0=1.5m时,A物体能追上B物体.

