问题描述：
如图，xOy坐标轴上有A（L，0）C（0，
L）两点．在△OCA区域内有垂直于xOy平面向里的匀强磁场B．一群质量为m、电荷量为q（q>0）的同种粒子（粒子间相互作用不计），同一时刻从OC边以平行于x轴方向射入磁场．粒子射入磁场前间距均匀（极小）、速度相同．从OC边射出的粒子占粒子总数75%．不计重力．下列说法正确的是（ ）
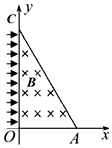
A. 粒子在磁场中按顺时针方向运动
B. 粒子在磁场中运动时间最长为
C. 粒子速度大小为
D. 粒子在磁场中运动时间最短为
最佳答案： 
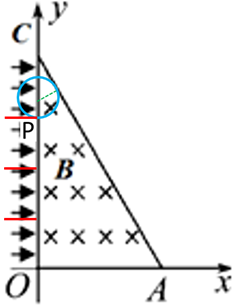A、用左手定则可以判断粒子在磁场中按逆时针方向运动，故A错误；
B、粒子在磁场中运动的周期为T=
，轨迹对应的圆心角最大值为θ=π，所以运动时间最长为t=
T=
，故B正确；
C、设从OC边P点入射的粒子恰能从OC边射出，半径为r，其轨迹恰好与AC相切，
因为C点坐标为（0，
L），所以OC=
L
因为粒子从OC边均匀射入，75%粒子能从OC边射出，故OC边75%长度射入的粒子能从OC射出，
即：从OP段入射的粒子均能从OC边射出，CP段入射粒子不能从OC边射出，
可知：CP=
OC=
L
根据几何关系可得：CP=r+
=
L
解得：粒子轨迹半径：r=
…①
根据洛伦兹力提供向心力可得：qvB=m
…②
联立①②式可得粒子速度大小：v=
，故C正确；
D、从C点入射的粒子在磁场中运动时间最短为0，故D错误；
故选：BC
