问题描述:
如图所示,在坐标系xOy的第一象限内斜线OC的上方存在垂直纸面向里的匀强磁场,磁感应强度为B,第四象限内存在磁感应强度大小未知,方向垂直纸面向里的匀强磁场,第三象限内存在沿y轴负方向的匀强电场,在x轴负半轴上有一接收屏GD,GD=20D=d,现有一带电粒子(不计重力)从y轴上的A点,以初速度v
0水平向右垂直射入匀强磁场,恰好垂直OC射出,并从x轴上的P点(未画出)进入第四象限内的匀强磁场,粒子经磁场偏转后又垂直y轴进入匀强电场并被接收屏接收,已知OC与x轴的夹角为37°,OA=
d,求:

(1)粒子的电性及比荷
;
(2)第四象限内匀强磁场的磁感应强度B′的大小;
(3)第三象限内匀强电场的电场强度E的大小范围.
 最佳答案:
最佳答案: (1)粒子运动轨迹如图所示:
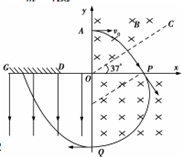
由左手定则可知,粒子带负电,
由几何知识可得,粒子在第一象限内做圆周运动的轨道半径:r=
d,
洛伦兹力提供粒子做圆周运动的向心力,
由牛顿第二定律得:qv0B=m
,解得:
=
;
(2)由图示粒子运动轨迹可知:OP=d,
粒子在第四象限内做圆周运动的轨道半径:R=
=
d,
由牛顿第二定律得:qv0B′=m
,解得:B′=
B;
(3)粒子在匀强电场中做类平抛运动,
由几何知识得:OQ=R+Rsin37°=2d,
E较大时粒子击中D点,由类平抛运动规律得:
d=v0t 2d=
t2,解得:Emax=
;
当E较小时,粒子击中G点,由类平抛运动规律得:
d=v0t 2d=
t2,解得:Emin=
,
电场强度范围:
≤E≤
;
答:(1)粒子带负电,粒子的比荷
为:
;
(2)第四象限内匀强磁场的磁感应强度B′的大小为
B;
(3)第三象限内匀强电场的电场强度E的大小范围是:
≤E≤
作业帮用户 2017-04-06 问题解析 - (1)根据题意作出粒子运动轨迹,由左手定则判断出粒子的电性,求出粒子做圆周运动的轨道半径,然后由牛顿第二定律求出粒子比荷.
(2)粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出磁感应强度.
(3)粒子在电场中做类平抛运动,应用类平抛运动规律求出电场强度的临界值,然后求出电场强度的范围.
名师点评 -
本题考点: 带电粒子在匀强磁场中的运动 带电粒子在匀强电场中的运动
-
考点点评: 本题考查了粒子在电场与磁场中的运动,粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的关键,应用牛顿第二定律与类平抛运动规律可以解题,解题是注意几何知识的应用.
 扫描下载二维码
扫描下载二维码



 扫描下载二维码
扫描下载二维码 