问题描述:
平面OM和水平面ON之间的夹角为30°,其横截面如图所示,平面OM和平面ON之间同时存在匀强磁场和匀强电场,磁感应强度大小为B,方向垂直于纸面向外.匀强电场的方向竖直向上,一带电小球的质量为m,电荷量为q,带电小球沿纸面以大小为v0的速度从OM的某点向左上方射入磁场,速度与OM成30°角,带电小球进入磁场后恰好做匀速圆周运动,已知粒子在磁场中的运动轨迹与ON恰好相切,且带电小球能从OM上另一点P射出磁场,(P未画出)求: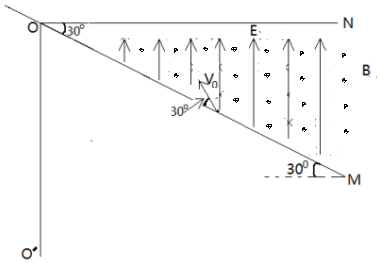
(1)判断带电小球带何种电荷?所加电场强度E为多大?
(2)带电小球离开磁场的射点P到两平面交点O的距离S多大?
(3)带电小球离开磁场后继续运动,能打在左侧竖直的光屏OO′,此点到O点的距离多大?
(1)小球在复合场中做匀速圆周运动,洛伦兹力提供向心力,
小球受到电场力与重力平衡,小球所受电场力竖直向上,
电场力方向与场强方向相同,则小球带正电荷;
电场力与重力大小相等:qE=mg,解得:E=
| mg |
| q |
(2)小球进入磁场后做匀速圆周运动,洛伦兹力作为向心力,
由牛顿第二定律得:qv0B=m
| ||
| r |
| mv0 |
| qB |
根据题意,带电小球在匀强磁场中的运动轨迹如图所示,
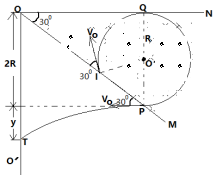
Q点为运动轨迹与ON相交的点,I点为入射点,P点为出射点,则IP为圆轨道的弦,
小球离开磁场的速度方向与OM的夹角也为300°,由几何关系可得,QP为圆轨道的直径,
所以,OP的长度S为:S=
| QP |
| sin30° |
| 2r |
| sin30° |
| 4mv0 |
| qB |
(3)带电小球从P点离开磁场后做平抛运动,
设打在光屏上的T点,竖直位移为y.
水平位移:x=v0t,解得:t=
| x |
| v0 |
| Scos30° |
| v0 |
2
| ||
| qB |
竖直位移:y=
| 1 |
| 2 |
| 6m2g |
| q2B2 |
如图所示,OT的距离H为:H=2R+y=
| 2mv0 |
| qB |
| 6m2g |
| q2B2 |
答:(1)带电小球带正电荷,所加电场强度E为
| mg |
| q |
(2)带电小球离开磁场的射点P到两平面交点O的距离S为
| 4mv0 |
| qB |
(3)带电小球离开磁场后继续运动,能打在左侧竖直的光屏OO′,此点到O点的距离为:
| 2mv0 |
| qB |
| 6m2g |
| q2B2 |

