如图所示，两平行竖直线MN、PQ间距离为a，其间存在垂直纸面向里的匀强磁场（含边界PQ），磁感应强度为B，在MN上O点处有一粒子源，能射出质量为m，电量为q的带负电粒子，当速度方向与OM

问题描述：

如图所示，两平行竖直线MN、PQ间距离为a，其间存在垂直纸面向里的匀强磁场（含边界PQ），磁感应强度为B，在MN上O点处有一粒子源，能射出质量为m，电量为q的带负电粒子，当速度方向与OM夹角θ=60°时，粒子恰好垂直PQ方向射出磁场，不计粒子间的相互作用及重力．则（　　）

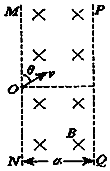
A. 粒子的速率为

qBa

m

B. 粒子在磁场中运动的时间为

πm

3qB

C. 若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则PQ边界上有粒子射出的区间长度为2

3

a

D. 若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则粒子在磁场中运动的最长时间为

3πm

qB

---

最佳答案：

A、当速度方向与OM夹角θ=60°时，粒子恰好垂直PQ方向射出磁场，则粒子做圆周运动的圆心在PQ上，如图所示，

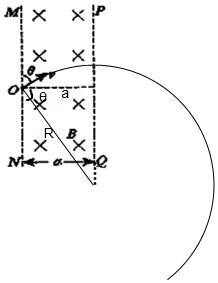
所以，Rcosθ=a，则R=2a；
粒子在磁场中做圆周运动，洛伦兹力做向心力即Bvq=

mv2

R

，所以，v=

BqR

m

=

2Bqa

m

；故A错误；
B、粒子在磁场中做圆周运动的周期T=

2πR

v

=

2πm

Bq

，又有粒子在磁场中转过的中心角为90°-θ=30°，所以，运动时间t=

30°

360°

T=

πm

6Bq

，故B错误；
C、当θ=0时，
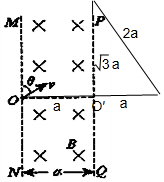
粒子在PQ边界上O′点上方

3

a处射出；当θ增大时，出射点下移，直到粒子运动轨迹与PQ相切；当粒子运动轨迹与PQ相切时，相切点位于O′点下方

3

a处；继续增大θ，粒子将从MN边界射出；故若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则PQ边界上有粒子射出的区间长度为2

3

a，故C正确；
D、当粒子运动轨迹与PQ相切时，粒子在MN的出射点位于O点下方2

3

a；若θ继续增大，则出射点沿MN边界上移，知道O点，故粒子在磁场中运动轨迹对应的最大弦长为2

3

a，所以，对应的最大中心角为120°，那么，若只改变粒子速度方向，使θ角能在0°至180°间不断变化，则粒子在磁场中运动的最长时间为

1

3

T=

2πm

3qB

，故D错误；
故选：C．