问题描述:
两根长均为L=1.00m的不可伸长绝缘轻线一端固定于天花板上的O点,另一端各自拴有质量均为m=1.00×10-2kg的带电小球A和B,已知A带负电、B带正电,电量大小均为q=1.00×10-7C,两球间用一长也为L的不可伸长绝缘轻线连接.天花板下方存在大小为E=1.00×106N/C的匀强电场,方向水平向右.A、B两球静止时的位置如图所示.现将O、B间的轻线烧断,由于存在空气阻力,A、B两球最后会再次静止在新的平衡位置.求:(忽略电荷间相互作用力,g取10m/s2)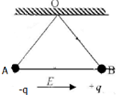
(1)在轻线OB烧断后,待A、B两球重新静止时,连接A、B的轻线中张力大小F1;
(2)从烧断OB开始,到系统重新达到平衡的过程中系统克服空气阻力做的功W.
(1)在细线OB烧断后,对B受力分析如图所示:
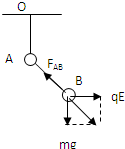
qE=1.00×10-7×1.00×106N=0.1N,
而mg=1.00×10-2×10N=0.1N
根据力的合成法则,结合勾股定理,则有:FAB=
| (qE)2+(mg)2 |
(2)AB线与水平方向夹角θ,
则tanθ=
| mg |
| qE |
所以 θ=45°
所以重力做功:WG=mgL(1-sin60°+1+sin45°-sin60°)=0.0975J
电场力做功:WE=qEL(-sin30°+sin45°-sin30°)=-0.0293J
所以克服阻力的功:Wf=WG+WE=0.0682J
答:(1)在轻线OB烧断后,待A、B两球重新静止时,连接A、B的轻线中张力大小为0.14N;
(2)从烧断OB开始,到系统重新达到平衡的过程中系统克服空气阻力做的功为0.0682J.

