如图所示，在水平圆盘上有一过圆心的光滑小槽，槽内有两根原长、劲度系数均相同的橡皮绳拉住一质量为m的小球，一条橡皮绳拴在O点，另一条拴在O′点，其中O为圆盘的中心，O′点在圆

问题描述：

如图所示，在水平 圆盘上有一过圆心的光滑小槽，槽内有两根原长、劲度系数均相同的橡皮绳拉住一质量为m的小球，一条橡皮绳拴在O点，另一条拴在O′点，其中O为圆盘的中心，O′点在圆盘的边缘上，橡皮绳的劲度系数为k，原长为圆盘半径R的

1

3

，现使圆盘角速度由零缓慢增大，则（　　）

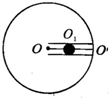
A. ω=

k 2m

时，OO′间橡皮绳处于原长

B. ω=

k 5m

时，小球距圆心距离为

5R

9

C. ω=

3k 5m

时，小球距圆心的距离为

5

6

R

D. ω=

3k 5m

时，OO₁间橡皮绳的弹力为kR

---

最佳答案：

A、当圆盘的角速度为ω0时，外侧橡皮绳恰好无拉力，则有：k(23R-13R)=m23Rω02，可得ω0=k2m，故A正确；B、k5m<k2m，则两橡皮绳均有拉力，设此时半径为r1，则有：k(r1-13R)-k(R-r1-13R)=mr1ω2解得：r1=5R9，故B...