问题描述:
如图,长为L的细线一端拴一个质量为m的小球A,另一端固定在O点,A静止时恰与光滑水平桌面接触,但无相互作用力,它可以绕O点在竖直平面内做圆周运动,另一个质量也是m的金属块B以初速在桌面上运动,并与A发生弹性正碰,求至少多大,B才能从右边滑出桌面?(A、B都可看作质点)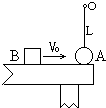
根据动量守恒定律可知,两球质量相等,碰撞后交换速度;故碰后,B静止,A做圆周运动;要使B能从右侧滑出,则A至少应过最高点,设它在最高点速度为v; 对A有:mg=mv2L; 由机械能守恒定律可知:12mv02=mg2L+12mv2碰后...

