如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，

问题描述：

如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，小球所受阻力做的功为W，重力加速度为g，则小球到达最低点时（　　）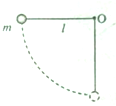

A. 向心加速度度a=

2(mgl+w)

ml

B. 向心加速度a=

2(mgl-w)

ml

C. 绳的拉力F=

3mgl+2w

l

D. 绳的拉力F=

2(mgl+w)

l

---

最佳答案：

A、根据动能定理得：mgL+W=

1

2

mv2，则向心加速度为：a=

v2

L

=

2(mgL+W)

mL

，故A正确，B错误．
C、在最低点，根据牛顿第二定律得：F-mg=m

v2

L

，解得绳子的拉力为：F=mg+m

v2

L

=

3mgL+2W

L

，故C正确，D错误．
故选：AC．