如图所示，宽为a的平行光束从空气斜射到平行玻璃砖上表面，入射角为60°，光束中包含两种波长的光，玻璃砖对这两种光的折射率分别为n1=3，n2=536，光束从玻璃下表面出射时恰好分成不重

问题描述：

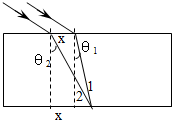
如图所示，宽为a的平行光束从空气斜射到平行玻璃砖上表面，入射角为60°，光束中包含两种波长的光，玻璃砖对这两种光的折射率分别为n₁=

3

，n₂=

5 3

6

，光束从玻璃下表面出射时恰好分成不重叠的两束，求玻璃砖的厚度d为多少？（已知sin37°=0.6，cos37°=0.8，结果可用根式表示）．

---

最佳答案：

根据光的折射定律，则有：n1=

sin60°

θ1

n2=

sin60°

θ2

，
得：θ1=30°θ2=37°             
由分析可知，恰好分开时：
x=d（tan37°-tan30°）      
又有：x=

a

cos60°

        
解得：d=

24a

9-4 3

=

24(9+4 3 )a

33

    

答：玻璃砖的厚度d为

24(9+4 3 )a

33

．