如图所示，质量M=1kg的木板在外力，的作用下，静置于倾角θ=30°、足够长的固定光滑斜面上．质量m=1kg的小物块（可视为质点）以初速度v=6.0m/s从木板的下端冲上木板，在此同时撤去外力F，

问题描述：

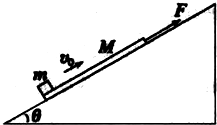
如图所示，质量M=1kg的木板在外力，的作用下，静置于倾角θ=30°、足够长的固定光滑斜面上．质量m=1kg的小物块（可视为质点）以初速度v=6.0m/s从木板的下端冲上木板，在此同时撤去外力F，（已知小物块与木板之间的动摩擦因数μ=

2

5

3

，重力加速度g=10m/s2）．

（1）在小物块刚冲入时，木块m和木板M的加速度．
（2）若小物块恰好不从木板的上端滑出，求木板的长度l为多少？
（3）木板M沿斜面向上位移的最大值．

---

最佳答案：

（1）小物块冲入后，木板受到的沿斜面向上的滑动摩擦力为：f=μmgcosθ=6N，
木板重力沿斜面向下的分力为：Gx=mgsinθ=5N
由于f>Gx，木板M将沿斜面向上滑动．
由（1）得木板M先向上加速，对M有：
Ma2=f-Gx
f=μmgcosθ
Gx=Mgsinθ
联立并代入数据解得：a2=1m/s2，方向沿斜面向上
对m有：
ma1=f+Gx1
f=μmgcosθ
Gx1=mgsinθ
联立并代入数据解得：a2=11m/s2，方向沿斜面向下
（2）小物块将向上减速到与木板M的速度相同的过程有：
v0-a1t1=v1
0+a2t1=v1
解得：t1=0.5s
v1=0.5m/s
所以，Sm=

v0+v1

2

t1
SM=

0+v1

2

t1
木板长为：
l=△s=Sm-SM=

v0

2

t1=1.5m
（3）设M、m速度相同后一起运动，则有：
a=gsinθ，
对m有：f静+mgsinθ=ma，
解得：f静=0<fm，假设合理，即m、M将一起上升．

S

′M

=

v 21

2a

=0.025m
所以SM+

S

′M

=0.15m
答：（1）在小物块刚冲入时，木块m和木板M的加速度分别为11m/s2，1m/s2，．
（2）若小物块恰好不从木板的上端滑出，木板的长度l为1.5m
（3）木板M沿斜面向上位移的最大值为0.15m．