问题描述:
如图所示,在匀强磁场的上方有一质量为m、半径为R的细导线做成的圆环,圆环的圆心与匀强磁场的上边界昀距离为h.将圆环由静止释放,圆环刚进入磁场的瞬间和完全进入磁场的瞬间,速度均为vo已知匀强磁场的磁感应强度为B,导体圆环的电阻为r,重力加速度为g,则下列说法正确的是( )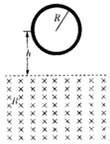
A. 圆环刚进入磁场的瞬间,速度v=
| 2g(h-R) |
B. 圆环进入磁场的过程中,电阻产生的热量为2mgR
C. 圆环进入磁场的过程中,通过导体横截面的电荷量为
| πBR2 |
| r |
D. 圆环进入磁场的过程做的是匀速直线运动
A、由图可知,圆环开始进入磁场时下落的高度为h-R,根据机械能守恒定律可知:mg(h-R)=
| 1 |
| 2 |
| 2g(h-R) |
B、由于圆环刚进入磁场的瞬间和完全进入磁场的瞬间速度相等,根据动能定理得:mg2R-W=0,所以W=2mgR.而克服安培力所做的功等于产生的热量,故B正确.
C、根据q=
| . |
| I |
| △Φ |
| r△t |
| △Φ |
| r |
| 0-πR2 |
| r |
| πBR2 |
| r |
| πBR2 |
| r |
D、由于圆环刚进入磁场的瞬间和完全进入磁场的瞬间速度相等,该过程感应电流不同,安培力不同,故线圈不可能匀速,故D错误;
故选:ABC

