如图甲所示，倾角为θ=30°绝缘斜面被垂直斜面直线MN分为左右两部分，左侧部分光滑，范围足够大，上方存在大小为E=1000N/C，方向沿斜面向上的匀强电场，右侧部分粗糙，范围足够大，一质

问题描述：

如图甲所示，倾角为θ=30°绝缘斜面被垂直斜面直线MN分为左右两部分，左侧部分光滑，范围足够大，上方存在大小为E=1000N/C，方向沿斜面向上的匀强电场，右侧部分粗糙，范围足够大，一质量为m=1kg，长为L=0.8m的绝缘体制成的均匀带正电直棒AB置于斜面上，A端距MN的距离为d，现给棒一个眼斜面向下的初速度v₀，并以此时作为计时的 起点，棒在最初0.8s的运动图象如图乙所示，已知0.8s末棒的B端刚好进入电场，取重力加速度g=10m/s²，求：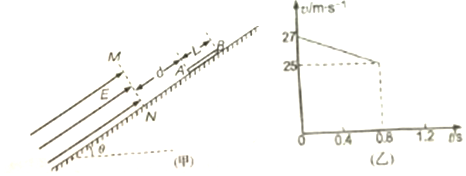

（1）直棒AB开始运动时A端距MN的距离为d；
（2）直棒AB的带电量q；
（3）直棒AB最终停止时，直棒B端到MN的距离．

---

最佳答案：

（1）0～0.8s内棒运动的位移为：
x1=

v0+v

2

t=

27+25

2

×0.8m=20.8m，
A端距离MN 的距离为：
d=x1-L=20.8-0.8m=20m．
由乙可知，棒在向左运动至B端刚好进入电场的过程中，棒的加速度一直不变，为：
a=

△v

△t

=2.5m/s2，
当B端刚进入电场时根据牛顿第二定律可得：
qE-mgsinθ=ma
得：q=

m(a+gsinθ)

E

=

1×(2.5+5)

1000

=7.5×10-3C．
（3）AB棒未进入电场前，根据牛顿第二定律可得：
μmgcosθ-mgsinθ=ma
代入数据解得：
μ=

a+gsinθ

gcosθ

=

3

2

从棒AB刚完全进入电场到B刚要离开电场的运动过程中，静电力做功为零，重力做功为零．而棒AB出电场过程中，因电场力做的正功与摩擦力做的负功大小相等，二力总功为零，
棒B端出电场直到最终停止，设B端在MN右侧与MN相距为x，由动能定理可得：
-mgxsinθ-μmgcosθ(x-L)=0-

1

2

m

v

2

，
代入数据求得：x=25.48m
故B端在MN右边且距MN为25.48m．
答：（1）直棒AB开始运动时A端距MN的距离为d为20m；
（2）直棒AB的带电量q为7.5×10-3C；
（3）直棒AB最终停止时，直棒B端到MN的距离为25.48m．