问题描述:
如图所示,为平衡箱可移动的塔式起重机简易示意图,它广泛用于楼房建筑中材料的输送及建筑构件的安装.平衡臂与起重臂可视为杠杆,O为支点,平衡臂最长为L1=10m、起重臂最长为L2=25m,平衡箱的质量为2×104kg.(平衡臂重、起重臂重、动滑轮重、绳重及吊钩重均不计,g取10N/kg)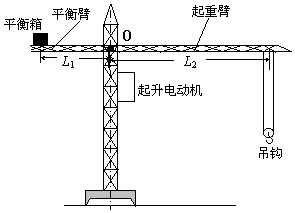
(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡箱的质量应越___.
(2)当吊钩在起重臂的最右端时(起重臂为最长),起重机能吊起货物的最大质量是___kg;接着,吊起最重的货物后,在电动机的牵引下,吊起的货物以2m/s的速度从起重臂的最右端向O点移动,同时平衡箱也以某一速度向O点移动,在确保起重机起重臂、平衡臂始终平衡的情况下,平衡箱移动的速度是多少?
(3)在某次起吊重为1.2×104N的货物过程中,将货物提升到30m的高度,用时50s,此过程起升电动机的效率为90%,则该起升电动机的实际功率是多少?
(4)在确保安全的情况下,该起重机在不起吊货物时,平衡箱应处在O点左面、O点右面还是O点?
1
(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可得:F2=
| F1L1 |
| L2 |
(2)配重物的重力G=mg=2×104kg×10N/kg=2×105N;
根据杠杆的平衡条件F1L1=F2L2可知,
起重机在最大起吊幅度时能吊起物体的重力G′=
| GL1 |
| L2 |
| 2×105N×10m |
| 25m |
由G=mg可得:m=
| G′ |
| g |
| 80000N |
| 10N/kg |
由图可知,有两段绳子吊着物体,
而v物=2m/s,
所以绳子末端移动的速度为:v绳=2v物=2×2m/s=4m/s
吊起最重的货物后,在电动机的牵引下,吊起的货物以2m/s的速度从起重臂的最右端向O点移动,同时平衡箱也以某一速度向O点移动,在此过程中,确保起重机起重臂、平衡臂始终平衡的情况下,根据杠杆的平衡条件F1L1=F2L2可得,
G′(L2-v绳t)=G(L1-vt),
80000N(25m-4m/st)=200000N(10m-vt),
解得v=1.6m/s;
(3)有用功W有用=Gh=1.2×104N×30m=3.6×105J,
总功W总=
| W有用 |
| η |
| 3.6×105J |
| 90% |
实际功率P=
| W总 |
| t |
| 4×105J |
| 50s |
(4)由于平衡臂重、起重臂重、动滑轮重、绳重及吊钩重均不计,根据杠杆的平衡原理,平衡箱应处在O点,因为无论处在左侧还是右侧杠杆都不会平衡,只有处在O点才能保持平衡,故应位于O点.
答:(1)大;
(2)8000kg;平衡箱移动的速度是1.6m/s;
(3)该起升电动机的实际功率是8000瓦;
(4)平衡箱应处在O点.

