问题描述:
一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴间夹角均为30°,小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m,c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,且与轴上P点、环c相连.当装置以某一转速转动时,弹簧伸长到| 3 |
| 2 |
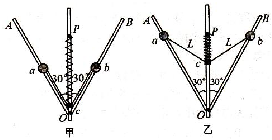
(1)细线刚好拉直而无张力时,装置转动的角速度ω1;
(2)如图乙所示,该装置以角速度ω2 (未知)匀速转动时,弹簧长为
| L |
| 2 |
(3)该装置转动的角速度由ω1缓慢变化到ω2,求该过程外界对转动装置做的功.
(1)小球做匀速圆周运动,由向心力公式有:
mgtan60°=mω12Lsin30°
解得:角速度ω1=
|
(2)对环c.由竖起方向力平衡得:2F线cos60°=mg+F弹;
由题,弹簧拉伸和压缩的形变量相同,则F弹=mg
对球a:竖直方向有 FNsin30°=mg+2F线sin30°
解得,弹力 FN=4mg
(3)球a做匀速圆周运动,根据向心力公式有:
FNcos30°+F线cos30°=mω22Lcos30°
a球的线速度 v2=ω2Lcos30°
整个过程弹簧弹性势能的变化量为零,弹簧弹力做的功为零,对系统,由功能关系得:
W=△Ep+△Ek=mg(
| 3L |
| 2 |
| L |
| 2 |
| 3L |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| L |
| 2 |
17-3
| ||
| 2 |
答:
(1)细线刚好拉直而无张力时,装置转动的角速度ω1是
|
(2)此时杆对小球的弹力大小是4mg;
(3)该装置转动的角速度由ω1缓慢变化到ω2,该过程外界对转动装置做的功是
17-3
| ||
| 2 |

