问题描述:
如图所示,让物体(可视为质点)从图中的C位置由静止开始做圆周运动,其运动轨迹的圆弧与地面相切于最低点D处,物体运动到D点时摆线刚好被拉断,物体在粗糙的水平面上由D点向右做匀减速运动,到达A孔进入半径R=0.36m的竖直放置的光滑圆轨道,当物体进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,物体质量为m=1.0kg,D点与小孔A的水平距离s=2m,g取10m/s2,试求: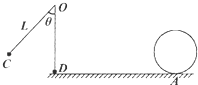
(1)物体在D点时的速度;
(2)如果物体能进入圆轨道并且恰好能通过轨道最高点,求粗糙水平面摩擦因数μ的值.
(1)当摆球由C到D运动,机械能守恒,则得:mg(L-Lcosθ)=
| 1 |
| 2 |
解得:vD=2
| 5 |
(2)若小球能过圆轨道的最高点则不会脱离轨道,在圆周的最高点由牛顿第二定律可得:mg=
| mv2 |
| R |
由动能定理可得:-μmgs-2mgR=
| 1 |
| 2 |
| 1 |
| 2 |
解得:μ=0.05
答:(1)物体在D点时的速度为2
| 5 |
(2)如果物体能进入圆轨道并且恰好能通过轨道最高点,粗糙水平面摩擦因数μ的值为0.05.

