问题描述:
图1为阿特武德机的示意图(不含光电门),它是早期测量重力加速度的器械,由英国数学家、物理学家阿特武德于1784年制成,他将质量均为M的重物用细绳连接后,放在光滑的轻质滑轮上,处于静止状态,再在一个重物上附加一质量为m的小重物,这时,由于小重物的重力而使系统做初速度为零的缓慢加速运动.测出其微小的加速度a,就可计算出重力加速度.(计算结果保留两位有效数字)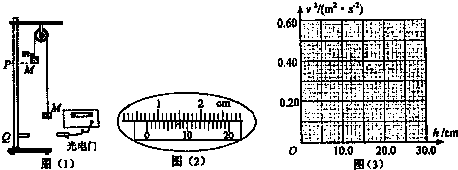
(1)依据实验原理,重力加速度可表示为g=___.(用物理量m、M、a表示)
(2)为测量物体下落的加速度,某同学在阿特武德机的竖直杆上的Q点加装了光电门,用其测量左侧物体经过光电门时的挡光时间△t.让物体从与杆上的另一点P同一高度处由静止下落,用h表示P、Q两点的高度差,用L表示左侧物体遮光部分的长度①用20分度的游标卡尺测量L时如图2所示,则L=___cm;
②某次实验中用光电门测出△t=1.85×l0-2s,则物体通过光电门时的速率v=___m/s;
③多次改变光电门的位置Q,每次均令物体从P点由静止开始运动,测量相应的h与△t的值,并计算出物体经过光电门时的瞬时速度v,下表是记录的几组实验数据,请根据实验数据在图3中作出v2一h的图象;
| v2/(m2•a-2) | 0.160 | 0.241 | 0.320 | 0.401 | 0.409 |
| h/m | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 |
⑤若M=1.10kg,m=0.20kg,则可得当地重力加速度的值为g=___m/s2.
(1)对整体分析,整体所受的合力大小为mg,则整体的加速度a=
| mg |
| 2M+m |
解得:g=
| 2M+m |
| m |
(2)游标卡尺的固定刻度读数为7mm,游标读数为0.05×8mm=0.40mm,
所以最终读数为:L=7mm+0.40mm=7.40mm=0.740cm,
极短时间内的平均速度表示瞬时速度,则
滑块经过光电门时的速度表达式v=
| L |
| △t |
| 0.740×10-2 |
| 1.85×10-2 |
(3)根据描点法做作出v2-h的图象,如图所示:
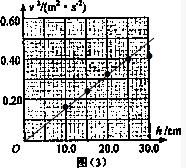
物体下落过程中,根据2ah=v2可知,v2-h的图象的斜率k=2a,
则2a=
| 0.40-0 |
| 0.25-0 |
解得:a=0.80m/s2,
根据(1)可知,g=
| 2M+m |
| m |
| 2×1.10+0.20 |
| 0.20 |
故答案为:(1)
| 2M+m |
| m |

