问题描述:
如图所示,半径R=1.0m、圆心角θ=106°的光滑圆轨道AC与粗糙的固定斜面相切于C点.A、C为圆弧的两端点,其连线水平,B为圆弧的最低点.质量m=0.1kg的小球以v0=5m/s的速度从A点沿切线方向进入圆弧轨道,离开G点后沿斜面运动最高可到达D点.小球与斜面间的动摩擦因数μ=| 1 |
| 3 |
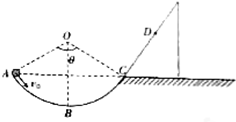
(1)小球经过B点时对轨道压力的大小;
(2)D点与C点的高度差.
(1)小球从A到B过程,由动能定理得:
mgR(1-cos
| θ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在B点,由牛顿第二定律得:F-mg=m
| ||
| R |
解得:F=4.3N,由牛顿第三定律可知,
小球对轨道的压力:F′=F=4.3N,方向:竖直向下;
(2)A、C等高,从A到D过程,由动能定理得:
-mgh-μmgcos
| θ |
| 2 |
| h | ||
sin
|
| 1 |
| 2 |
答:(1)小球经过B点时对轨道压力的大小为4.3N;
(2)D点与C点的高度差为1m.

