如图所示，电阻不计的两金属导轨相距为l，固定在水平绝缘桌面上，斜面MNPQ与水平直轨道在最低点相切，水平直导轨部分处在磁感应强度大小为B、方向竖直向下的匀强磁场中，末端与桌面

问题描述：

如图所示，电阻不计的两金属导轨相距为l，固定在水平绝缘桌面上，斜面MNPQ与水平直轨道在最低点相切，水平直导轨部分处在磁感应强度大小为B、方向竖直向下的匀强磁场中，末端与桌面边缘平齐，一质量为m、电阻为R的导体棒ab从距水平桌面的高度为h处无初速度释放，进入水平直导轨后向右运动，最后离开导轨落到水平地面上，落地点到桌面边缘的水平距离为x．已知斜面与水平面间的夹角为θ，PM处所接电阻的阻值也为R，且导体棒ab通过磁场的过程中通过它的电荷量为q，导体棒与导轨之间的动摩擦因数均为μ，桌面离地面的高度为H，重力加速度为g．求：

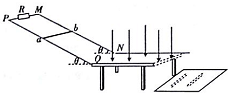
（1）导体棒进入磁场和离开磁场时的速度大小；
（2）导体棒在磁场中运动的过程中，回路产生的焦耳热．

---

最佳答案：

（1）设导体棒进入磁场和离开磁场时的速度大小分别为v1和v2
由动能定理有：mgh-μmgcosθ×

h

sinθ

=

1

2

m

v

21

解得：v1=

2gh(sinθ-μcosθ) sinθ

由平抛运动规律可知：x=v2t
H=

1

2

gt2
解得：v2=x

g 2H

（2）设导体棒在磁场中运动的位移为s，则由法拉第电磁感应定律有：
E=

△∅

△t

=

B△s

△t

=

Bls

△t

q=I△t
I=

E

2R

可得：s=

2qR

Bl

根据能的转化与守恒定得：

1

2

m

v

21

-

1

2

m

v

22

=μmgs+Q
解得：Q=mg(h-

μhcosθ

sinθ

-

x2

4H

-

2μgR

Bl

)
答：（1）导体棒进入磁场和离开磁场时的速度大小分别为：

2gh(sinθ-μcosθ) sinθ

和x

g 2H

；
（2）导体棒在磁场中运动的过程中，回路产生的焦耳热为mg(h-

μhcosθ

sinθ

-

x2

4H

-

2μgR

Bl

)．