问题描述:
如图所示,一质量M=20kg,倾角为θ=30°的三角形斜劈A放在水平地面上,质量m=10kg的物体B静止在斜劈上,处于水平位置的轻弹簧一端固定于墙壁,另一端与物体B相连,此时轻弹簧处于自然状态,其劲度系数k=250N/m.已知A与B之间的动摩擦因数为
| ||
| 2 |
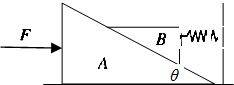
A. A、B两物体一直相对静止
B. A、B两物体之间的摩擦力先增大后减小
C. 推力F从零逐渐增大到125N
D. A、B两物体间的静摩擦力先做正功后做负功
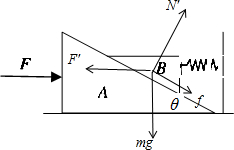
A、 对B受力分析,初状态如图,知f向上大小为f=mgsin30°=100×
对B受力分析,初状态如图,知f向上大小为f=mgsin30°=100×
| 1 |
| 2 |
当向右匀速运动0.5m,B的受力如图,
F′=kl=250×0.5=125N
F′cos30°>mgsin30°,故摩擦力向下,
最大静摩擦力fm=μ(mgcos30°+F′sin30°)=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
 ,AB一直相对静止,故A正确;
,AB一直相对静止,故A正确;B、根据受力分析知f先沿斜面向上,后沿斜面向下,知摩擦力先减小后增大,故B错误;
C、根据胡克定律F′=kx知形变量增大,弹力从零开始增大,对整体受力分析知F=f地+F′=μ(M+m)g+F′,F不是从零开始增大,故C错误;
D、根据W=FLcosα知摩擦力对A先做负功后做正功,故D错误
故选:A

