工人师傅利用如图所示的两种方式，将重均为300N的货物从图示位置向上缓慢提升一段距离．F1、F2始终沿竖直方向；图甲中OB=2OA，图乙中动滑轮重为60N，重物上升速度为0.01m/s．不计杠杆重、

问题描述：

工人师傅利用如图所示的两种方式，将重均为300N的货物从图示位置向上缓慢提升一段距离．F₁、F₂始终沿竖直方向；图甲中OB=2OA，图乙中动滑轮重为60N，重物上升速度为0.01m/s．不计杠杆重、绳重和摩擦，则下列说法正确的是（　　）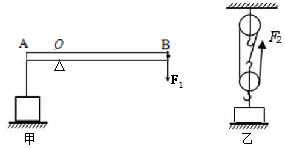

A. 甲乙两种方式都省一半的力

B. 甲方式F₁由150N逐渐变大

C. 乙方式机械效率约为83.3%

D. 乙方式F₂的功率为3W

---

最佳答案：

A、由甲图可知，OB=2OA，即动力臂为阻力臂的2倍，由于不计摩擦、杠杆自重，由杠杆平衡条件可知，动力为阻力的一半，即F1=150N；
由图乙可知，n=3，不计绳重和摩擦，则F2=

1

3

（G+G动）=

1

3

（300N+60N）=120N，故A错误；
B、甲图中，重力即阻力的方向是竖直向下的，动力的方向也是竖直向下的，在提升重物的过程中，动力臂和阻力臂的比值不变，故动力F1的大小不变，故B错误；
C、不计绳重和摩擦，则乙方式机械效率为：
η=

W有

W总

=

W有

W有+W额

=

Gh

Gh+G轮h

=

G

G+G轮

=

300N

300N+60N

=83.3%，故C正确；
D、乙方式中F2=120N，绳子的自由端的速度为v绳=0.01m/s×3=0.03m/s，
则乙方式F2的功率为：P=F2v绳=120N×0.03m/s=3.6W，故D错误．
故选：C．