问题描述：
如图所示，平面直角坐标系的第二象限内存在水平向左的匀强电场和垂直纸面向里的匀强磁场，一质量为m、带电荷量为+q的小球从A点以初速度v0沿直线AO运动，AO与x轴负方向成37°角，在y轴与MN之间的区域Ⅰ内加一电场强度最小的匀强电场后，可使小球继续做直线运动到MN上的C点，MN与PQ之间区域Ⅱ内存在宽度为d的竖直向上匀强电场和垂直纸面向里的匀强磁场，小球在区域Ⅱ内做匀速圆周运动并恰好不能从右边界飞出，已知小球在C点的速度大小为2v0，重力加速度为g，sin37°=0.6，cos37°=0.8，求：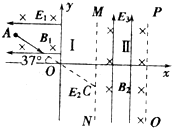
（1）第二象限内电场强度E1的大小和磁感应强度B1的大小；
（2）区域Ⅰ内最小电场强度E2的大小和方向；
（3）区域Ⅱ内电场强度E3的大小和磁感应强度B2的大小．
最佳答案： 
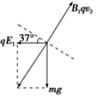（1）带电小球在第二象限内受重力、电场力和洛伦兹力做直线运动，三力满足如图所示关系且小球只能做匀速直线运动，由图知：
tan37°=
| qE2 |
| mg |
| 3mg |
| 4q |
cos37°=
| mg |
| B1qv0 |
得：B1=
| 5mg |
| 4qv0 |
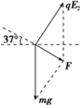
（2）区域Ⅰ中小球做直线运动，电场强度最小，受力如图所示（电场力方向与速度方向垂直），小球做匀加速直线运动，
由图知：cos37°=
| qE2 |
| mg |
| 4mg |
| 5q |
方向与x轴正方向成53° 向上．
（3）小球在区域Ⅱ内做匀速圆周运动，所以：
mg=qE3 得E3=
| mg |
| q |
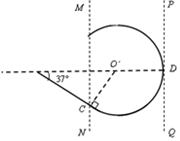
因为小球恰好不从右边界穿出，小球运动轨迹如图所示，由几何关系得：r=
| 5 |
| 8 |
由洛仑兹力提供向心力知：B2q2v0=m
| (2v0)2 |
| r |
联立得 B2=
| 16mv0 |
| 5qd |
答：（1）第二象限内电场强度E1的大小是
| 3mg |
| 4q |
| 5mg |
| 4qv0 |
（2）区域Ⅰ内最小电场强度E2的大小为
| 4mg |
| 5q |
（3）区域Ⅱ内电场强度E3的大小和磁感应强度B2的大小
| 16mv0 |
| 5qd |
