问题描述:
将一长方体甲竖直放在密度为ρ的某液体中时处于漂浮状态,且有
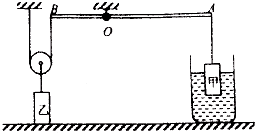
的体积露出页液面.另有一轻质杠杆AOB(O为支点),且OA=2OB,现用细线将长方体甲悬挂在杠杆的A端(如图所示),再用另一细线的一段系在杠杆的B端,另一端绕过一轻质滑轮悬挂在天花板上,轻质动滑轮下悬挂一个与甲完全相同的长方体乙并放在水平地面上.当轻质杠杆A、B两端细线均被拉直且杠杆水平平衡时,长方体甲有
的体积露出页面,已知长方体甲所在容器的内底面受到的液体压强为1000Pa(杠杆质量、动滑轮质量、细线质量及一切摩擦均不计).求:
(1)长方体的密度与液体的密度之比;
(2)长方体乙对地面的压强为多少?
 最佳答案:
最佳答案: (1)设物体的体积为V,当长方体漂浮时,有G=F ①
即ρ物gV=ρg
V ②
∴
=
(2)对长方体甲、细线拉力FA=G-F浮=ρg
V-ρg
V=
ρgV
由杠杆平衡条件,FA•OA=FB•OB,且OA=2OB,得2FA=FB
对长方体乙,有支持力FN=G-2FB=G-4FA=
ρgv
设长方体底面积为S 则压强P=
=
设长文体高为h,则p=
ρgh
由题意,ρg
h=1000Pa
故 P=
×
1000Pa=800Pa
答:(1)长方体密度与液体密度之比为4:5
(2)长方体对地面压强为800Pa


