问题描述：
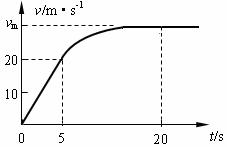
一新型赛车在水平专用测试道上进行测试，该车总质量为 m = 1×10 3 kg ，由静止开始沿水平测试道运动，用传感设备记录其运动的 v － t 图象如图所示。该车运动中受到的摩擦阻力（含空气阻力）恒定，且摩擦阻力跟车的重力的比值为 μ ＝ 0 ． 2 。赛车在 0 ～ 5s 的 v － t 图象为直线， 5s 末该车发动机达到额定功率并保持该功率行驶，在 5s ～ 20s 之间，赛车的 v － t 图象先是一段曲线，后为直线。取 g=10m/s 2 ，试求：
（ 1 ）该车额定功率；
（ 2 ）该车的最大速度 v m ；
（ 3 ）该车出发后前 20s 内的位移。
最佳答案： 答案： （ 1 ） 1 ． 2×10 5 W （ 2 ） 60m/s （ 3 ） 150 m
解 ：（ 1 ） 0s— 5s 赛车做匀加速运动，其加速度：
=4m/s 2 （ 1 分）
由题意得 
，得摩擦阻力 f= 2×10 3 N ， （ 1 分）
由牛顿定律： F － f =ma ， 得牵引力 F= 6×10 3 N （ 2 分）
所以， 发动机牵引力的额定功率 P=Fv 1 =1 ． 2×10 5 W （ 2 分）
（ 2 ） 由 
（ 2 分）
解得： v m =60m/s （ 1 分）
（ 3 ）前 5s 的位移： 
m （ 1 分）
在 5s ～ 20s 内（即 t 2 =15s ），发动机已经达到额定牵引功率，且在 20s 时车的速度已达到最大速度 v m ，由动能定理得：
（ 2 分）
代入数据解得 
m （ 1 分）
总位移 
m （ 1 分）
