如图甲所示，轻弹簧竖直固定在水平面上处于自由状态，一质量为m=0.2kg的小球，从弹簧上端某高度处自由下落，从它接触弹簧到弹簧压缩至最短的过程中（弹簧在弹性限度内），其速度u和

问题描述：

如图甲所示，轻弹簧竖直固定在水平面上处于自由状态，一质量为m=0.2kg的小球，从弹簧上端某高度处自由下落，从它接触弹簧到弹簧压缩至最短的过程中（弹簧在弹性限度内），其速度u和弹簧压缩量△x之间的函数图象如图乙所示，其中A为曲线的最高点，小球和弹簧接触瞬间机械能损失不计，取g=10m/s²，则（　　）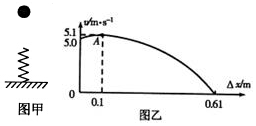

A. 当△x=0.1m时，小球处于失重状态

B. 小球在最低点时的加速度大于10m/s²

C. 从接触弹簧到压缩至最短的过程中，小球的机械能守恒

D. 小球从速度最大到压缩至最短，弹簧弹性势能增加量为3.621J

---

最佳答案：

A、由小球的速度图象知，开始小球的速度增大，小球的重力大于弹簧对它的弹力，当△x为0.1m时，小球的速度最大，然后速度减小，说明重力小于弹力，当△x=0.1m时，小球的重力等于弹簧对它的弹力，合力为零，小球的加速度为零，小球处于平衡状态，故A错误；
B、当△x=0.1m时，小球的重力等于弹簧对它的弹力，合力为零，根据对称性可知在压缩0.1m时，弹簧的弹力将增大mg，由于最终的压缩量大于0.2m，故弹簧的弹力大于2mg，故加速度小球在最低点时的加速度大于10m/s2，故B正确；
C、从接触弹簧到压缩至最短的过程中，弹簧的弹力对小球做负功，故小球的机械能不守恒，故C错误；
D、小球从速度最大到压缩至最短，弹簧弹性势能增加量为△Ep=

1

2

mv2+mgh=

1

2

×0.2×5．12+0.2×10×0.512J=3.621J，故D正确
故选：BD