问题描述:
卫己知AB平行cD,ADBc交于E,F在ED上,且角CBF等于角D,求证FB平方等于EF乘FA,若BF为3EF为2求三角形ABE与三角形BEF面积之比
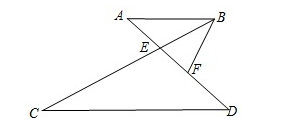
(1)证明:∵AB∥CD,
∴∠A=∠D.
又∵∠CBF=∠D,
∴∠A=∠CBF,
∵∠BFE=∠AFB,
∴△FBE∽△FAB,
∴FB/FA=FE/FB
∴FB2=FExFA;
解题思路:先证两个三角形相似,就能证明FB平方等于EFxFA
(2)∵FB2=FExFA,BF=3,EF=2
∴32=2×(2+AE)
∴AE=5/2
AE/EF=5/4
∴△ABE与△BEF的面积之比为5:4.
解题思路:已知BF=3,EF=2,可以求出三角形ABE与三角形BEF的面积之比

