问题描述：
如图d是三角形abc中角bca的外角角平分线与ba延长线上的交点 ，求证角bac大于角b。
最佳答案： 
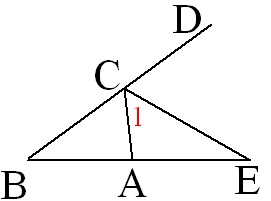
方法一
根据三角形外角定理有：
∠D+∠DCA=∠BAC
∠D+∠B=∠DCE=∠DCA
所以：
∠D+∠D+∠B=∠BAC
所以：2∠D=∠BAC-∠B＞0
所以：∠BAC＞∠B
方法二
∵∠ACD是ΔABC外角，∴∠ACD=∠B+∠BAC，
∵CE是角平分线，
∴∠ACD=2∠1，
∴2∠1=∠B+∠BAC，
∵∠BAC是ΔACE外角，
∴∠BAC>∠1，
∴2∠BAC>2∠1，
2∠BAC>∠B+∠BAC，
∴∠BAC>∠B。
