问题描述:
有一个由11个大小不同的正方形组成的完美长方形,其中最小正方形的边长为9,求此长方形的边长
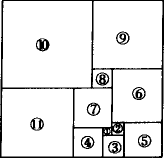
方法一
解:如图,给图中的小正方形编上号.①号正方形的边长是9 mm.设②号正方形的边长为x mm,则③号的边长为(x+9)mm;④号的边长为(x+9)+9=(x+18)mm;⑤号的边长为x+(x+9)=(2x+9)mm;⑥号的边长为x+(2x+9)=(3x+9)mm;⑦号的边长为(x+18)+9=(x+27)mm;⑧号的边长为(2x+9)+(3x+9)-(x+27)-(x+18)=(3x-27)mm;⑨号的边长为(3x-27)+(3x+9)=(6x-18)mm;⑩号的边长为(6x-18)+(3x-27)=(9x-45)mm;号的边长为(x+27)+(x+18)=(2x+45)mm.
注意到矩形的一边由⑩、⑨的正方形的边组成,长为(9x-45)+(6x-18)=(15x-63),又可由、④、③、⑤四个正方形的边组成,长为(2x+45)+(x+18)+(x+9)+(2x+9)=6x+81.
故15x-63=(6x+81).
解上述方程得x=16,进而可得矩形的边长为15×16-63=177(mm)及(9x-45)+(2x+45)=11x=11×16=176(mm).
答:矩形的边长分别为177 mm、176 mm.
方法二
设⑵的边长为x,则:
⑶的边长为x+9
⑷的边长为x+x+9=2x+9
⑸的边长为x+2x+9=3x+9
⑹的边长为9+x+9=x+18
⑺的边长为x+18+9=x+27
⑻的边长为x+18+x+27=2x+45
而⑷、⑸的边长和减去⑹、⑺的边长和即为⑼的边长,因此⑼的边长为:[(2x+9)+(3x+9)]-[(x+18)+(x+27)]=3x-27
⑽的边长为3x-27+3x+9=6x-18
⑾的边长6x-18+3x-27=9x-45
再由⑽、⑾的边长和=矩形的一边长=⑻、⑺、⑸的边长和可列方程:
6x-18+9x-45=2x+45+x+27+3x+9
解得:x=16
从而矩形的一边长为15x-63=177
相邻边长为:9x-45+2x+45=11x=176

