问题描述：
如图，己知三角形ABD全等三角形ADE，BC的延长线交DA于点F，交DE于点G，E
最佳答案： 
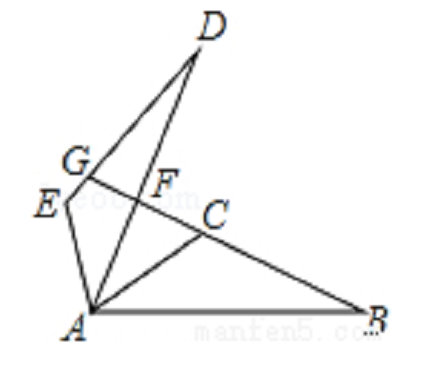
解法一：
解：
∵△ABC≌△ADE
∴∠ACB=∠E=105°
∴∠ACF=180°-105°=75°
在△ACF和△DGF中，∠D+∠DGB=∠DAC+∠ACF
即25+∠DGB=16°+75°
解得∠DGB=66°
解法二：
∵△ABC≌△ADE
∴∠ACB=∠E=105°
∴∠ACF=180°-105°=75°
∵∠DAC=16°
∴∠DFG=∠CFA=180°-75°-16°=89°
又∵∠D=25°
∴∠DGB=180°-25°-89°=66°
