我市某服装厂主要做外贸服装，由于技术改良，2012年全年每月的产量y（单位：万件）与月份x之间可以用如图所示的一次函数表示，但由于“欧债危机”的影响，销售受困，为了不使货积压

问题描述：

我市某服装厂主要做外贸服装，由于技术改良，2012年全年每月的产量y（单位：万件）与月份x之间可以用如图所示的一次函数表示，但由于“欧债危机”的影响，销售受困，为了不使货积压，老板只能是降低利润销售，原来每件可赚10元，从1月开始每月每件降低0.5元．试求：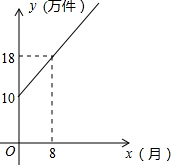

（1）y与x的函数关系式．
（2）几月份的单月利润是108万元？
（3）单月最大利润是多少？是哪个月份？

---

最佳答案：

（1）设所求的y与x之间的函数解析式y=kx=b，
∵图象过（0，10），（8，18）两点，
∴

b=10 8k+b=18

，
解得

k=1 b=10

．
∴y=x+10．
（2）由题意得：（10-0.5x）（x+10）=108，
∴-0.5x2+5x-9=0，
∴x2-10x+16=0，
∴（x-2）（x-8）=0，
解得：x1=2，x2=8．
答：2月份和8月份单月利润都是108万元．
（3）设利润为w，则
w=（10-0.5x）（x+10）
=-0.5x2+5x+100
=-0.5（x-5）2+112.5，
∴当x=5时，w有最大值112.5．
答：5月份的单月利润最大，最大利润为112.5万元．