问题描述：
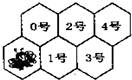有一排蜂房，形状如图，一只蜜蜂在左下角，假定蜜蜂只能爬行，不能飞，而且始终向右方（包括右上，右下）爬行，从一间蜂房爬到右边相邻的蜂房中去．例如．蜜蜂爬到1号蜂房的爬法有：蜜蜂→1号；蜜蜂→0号→1号，共有2种不同的爬法．问蜜蜂从最初位置爬到4号蜂房共有（ ）种不同的爬法． 
最佳答案：
分析：
画树状图，即可得到蜜蜂从最初位置爬到4号蜂房的所有的不同爬法．
画树状图如下：
蜜蜂从最初位置爬到4号蜂房共有8种可能的行走路线．
所以n=8．
故选：B．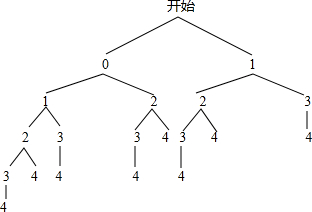
点评：
本题用树状图展示所有可能的结果比较容易得出结论，希望同学们能够掌握此法．
