问题描述:
如图,BE是 O的直径,点A,C,D,F都在 O上, |
| AE |
 |
| CD |
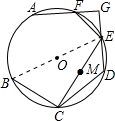
(1)若∠CDE=120°,CE=4
| 3 |
(2)求证:2FE=CE.
(3)试探索:在
 |
| AB |
(1)如图1,连接OM,OC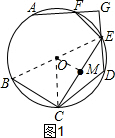
∵∠CDE=120°,
∴∠CBE=60°,
∴∠COE=120°,
∵M是CE的中点,
∴∠MOE=60°,∠OME=90°,
∵CE=4
| 3 |
∴EM=2
| 3 |
∴OE=4,
∴ O的周长为2π×OE=8π.
(2)如图2,连接AD,

∵F恰为AG的中点,EG=DE,
∴2EF=AD,
∵
 |
| AE |
 |
| CD |
∴
 |
| AD |
 |
| CE |
∴AD=CE,
∴2FE=CE.
(3)在
 |
| AB |
理由如下:
如图3,连接FM,过点E作EN⊥FM,
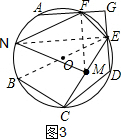
∵EF=EM,由(1)可得,
∴EN⊥FM,且平分FM,
∴在
 |
| AB |

