问题描述:
f(x),g(x)是定义在[a,b]上的连续函数,则“f(x)的最大值小于g(x)的最小值”是“f(x)<g(x)对一切x∈[a,b]成立”的( )A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 非充分非必要条件
若“f(x)的最大值小于g(x)的最小值”是“f(x)<g(x)对一切x∈[a,b]成立,即充分性成立,
反之不一定成立,比如g(x)=|x|+1,和f(x)=|x|,则不成立,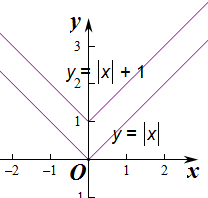
即“f(x)的最大值小于g(x)的最小值”是“f(x)<g(x)对一切x∈[a,b]成立”的充分不必要条件,
故选:A.

